INTERNATIONAL JOURNAL MARKETING BEHAVIOUR

Incomplete Credit Markets and Commodity Marketing Behaviour

Emma C. Stephens, Christopher B. Barrett

(Original submitted September 2009, revision received and accepted August 2010.)

Abstract

We use a simple theoretical model of seasonal market participation in the presence of liquidity constraints and transaction costs to explain the ‘sell low, buy high’ puzzle in which some households do not take advantage of inter-temporal price arbitrage through storage and sell output postharvest at prices lower than observed prices for purchases in the subsequent lean season. We test our model with data from western Kenya using maximum likelihood estimation of a multivariate sample selection model of market participation. Access to off-farm income and credit indeed seem to influence crop sales and purchase behaviours in a manner consistent with the hypothesised patterns.

Keywords: Commodity markets; inter-temporal arbitrage; Kenya; liquidity; maize; seasonality; storage.

JEL classifications: O13, O12, Q12, D91.

Introduction 1

Regular, sharp seasonal price fluctuations are a common characteristic of staple grains markets in many developing countries (Sahn, 1989). Yet many farmers appear not to take advantage of the apparent inter-temporal arbitrage opportunities created by predictable seasonal price variation in storable commodities. Instead, they often sell their output at low prices postharvest and buy back identical commodities several months later for prices far higher than they received postharvest.²
Several candidate reasons exist that might explain this ‘sell low, buy high’ puzzle, which is clearly at odds with unconstrained, inter-temporal profit-maximising behaviour (on which, see Williams and Wright, 1991). First, impatience could lead to very low storage rates of staple commodities. However, seasonal price increases often so far exceed prevailing local interest rates that this explanation frequently seems implausible. For example, in Kenya in the 2002–2003 crop year the mean annual change in maize prices across three large market centres (Bungoma, Kisumu and Nairobi) was 44%, while the mean bank deposit rate was only 5% (Central Bank of Kenya, 2004; IGAD, 2007). Furthermore, we routinely observe households in the study area investing in calves or other immature livestock, in children’s education that will pay off only with a long lag, and in other long-term ventures; there is plainly a general willingness to invest, just not necessarily in holding grains stocks inter-seasonally. Given such patterns and continuous household demand for basic grains for survival, it seems implausible that discount rates could be high enough to broadly explain the ‘sell low, buy high’ puzzle.
Second, appropriate storage technologies might not be available, raising inter-temporal storage costs to the point that storing output for future sale becomes unprofitable. But even at high inter-seasonal storage loss rates of 10–30% that might approach the observed maize price spreads in Kenya,³ the preceding argument still applies; one would need an implausibly high discount rate to make ‘sell low, buy high’ an attractive strategy. Moreover, evidence more often suggests that there are relatively inexpensive grains storage technologies available that reliably exhibit annual loss rates of only 1–2% (Barrett, 1997).⁴ Given this and the predictability of sharp seasonal price increases, there would seem to be high returns to investment in better household-level storage technologies that would obviate such explanations. The low storage quality explanation of ‘sell low, buy high’ marketing patterns therefore also seems implausible.
A third possible explanation for low storage demand could be longer-term concerns about price risk over several growing seasons. However, Saha and Stroud (1994), Barrett and Dorosh (1996) and Park (2006) have all explored the role of grain storage as a price hedge ex ante and find analytical and empirical support for storage patterns that also run contrary to the ‘sell low, buy high’ puzzle. They show that price risk aversion should generate excessive, rather than insufficient, stockholding postharvest.
An alternative class of intuitive explanations little explored empirically in the literature to date is that the ‘sell low, buy high’ phenomenon represents a ‘displaced distortion’ (Barrett, 2007) arising because of financial market failures that people implicitly resolve through seemingly irrational resource allocation patterns. If people have no other means of addressing temporary liquidity constraints, they might find it optimal to convert non-cash wealth in the form of grains into cash, even knowing that they will need to buy back grain later at a higher price, with the associated losses representing the de facto interest rate on a quasi-loan for several months. In this article, we develop that line of argument by innovatively combining models of consumption smoothing under liquidity constraints (Schechtman and Escudero, 1977; Zeldes, 1989; Deaton, 1991), with the literature on market participation (de Janvry et al., 1991; Goetz, 1992; Key et al., 2000; Bellemare and Barrett, 2006) to explore commodity marketing and storage behaviour that cumulatively result in ‘sell low, buy high’ grain marketing patterns. We show that liquidity constraints can lead to greater seasonal variability in shadow prices for agricultural output and that this instability can lead to seemingly perverse marketing behaviour, with liquidity-constrained households most at risk for failing to seize inter-temporal arbitrage opportunities through seasonal grain storage. We then test the hypotheses generated by this model econometrically using data on seasonal maize marketing patterns among farmers in western Kenya.

Theoretical Framework 2

The agricultural households in this study are assumed to maximise their expected utility of consumption of on-farm produced grains and other consumption goods that must be purchased with cash in the marketplace. Because of the seasonal nature of agricultural production, the household must decide how to satisfy these consumption needs both in each year’s harvest period, when household grain production is realised, as well as in the subsequent ‘lean’ period that falls between successive grain harvests. Starting with existing work, such as Saha’s (1994) two-period household model, we introduce the implications of both liquidity constraints and marketing transaction costs on the household’s two-period seasonal optimisation problem. The combination of existing two-period household models with the market participation and credit constraint literature into a single model makes it easy to distinguish the distinct inter-year market participation dynamics for the credit and non-credit constrained and identify some of the consequences of such marketing patterns in a manner not previously addressed in either the market participation or seasonality literature.
Households obtain utility from consuming staple grains (c_t) as well as a composite tradable good (x_t) that can only be purchased in the market. Every year, households maximise their utility through choices on harvest and lean period consumption [c_t, x_t for each period t = harvest (H), lean (L)]:

       (1)

where E_H is the expectations operator in the harvest period. At harvest time, the household realises its level of grain output, Q^* which is determined by input decisions in the previous year’s lean season. At this time, the household can choose to consume grain (c_H), store it until the lean season (S_H) or use it to purchase this season’s market good (x_H). The level of consumption at harvest time is thus constrained by the household’s full income, Y_H, such that:

(2)

and

(3)

where wL is the value of the household’s labour endowment net of any hired-in labour.⁵
In the lean season, household consumption is constrained by the level of stored grain from the harvest period (which depreciates at a rate of ν) and its labour endowment such that the full income constraint in the lean season is:

(4)

The behavioural result of optimisation problem (1) is a system of consumption demand equation (5) that are functions of current period and expected next period prices, as well as current and expected realisations of full income, Y_t (Antle and Capalbo, 2001)⁶:

(5)

We assume that current consumption is decreasing in all own prices as well as in the ratio of current to expected future own prices, and increasing in current and future incomes.
The two-period problem also results in a sequence of output supply equations for the harvest and lean seasons (q_H, q_L) that depend on harvest period grain production as well as the between-season storage decision:

(6)

Following Deaton (1991), one can readily adapt the solution to equation (1) to include the ability to borrow and save cash every period (b_t) as well as the possibility of a liquidity constraint α such that b_t ≤ α. Let Y(α) be the household’s full income when the liquidity constraint binds. The liquidity constraint implies that if full income Y_t falls below some threshold level, then a liquidity-constrained household can do no better than consume all of its available resources. On the consumption demand side, a discontinuity emerges in this case. If the household’s income realisation at harvest time is above the threshold, Y_H^*(α), which depends on the borrowing ceiling the household faces, then it will still smooth consumption by equating harvest and lean season expected marginal utility and the demand functions are as in equation (5). If, however, harvest income falls below the threshold (due, e.g. to seasonal variation in income and a low borrowing ceiling), the household cannot afford as much current consumption as it would choose in an unconstrained world. Therefore, the marginal utility of harvest season consumption exceeds the expected marginal utility of lean season consumption, inducing the household to do everything it can to minimise this gap, including liquidating carryover stocks. The consumption demand function for c_H can thus be written as follows:

(7)

The key point to note about this demand function is that when household income falls below the threshold, future prices and future income no longer affect consumption choice because optimal stock-out breaks the linkage. The household consumes all its available resources, irrespective of expected change in prices over time. Because the liquidity constraint creates a kink in the Euler equation that disrupts equilibration of marginal utility across periods, it likewise obviates the standard inter-temporal arbitrage conditions that guide household behaviour. Hence the basic intuition behind our model of the ‘sell low, buy high’ phenomenon: that liquidity-constrained households may optimally sell when prices are low not because they do not recognise predictable seasonal appreciation in the value of storable grain stocks but, rather, because their current income and expenditure needs force liquidation of their entire asset stock, rendering inter-temporal arbitrage opportunities irrelevant.
The presence of physical grain storage in the model does not change this fundamental point. When both physical and financial assets exist, the household chooses the form in which to hold its wealth: either as cash savings or as stored grain (Park, 2006). The optimal asset allocation then depends on the relative returns to different assets, on risk preferences, etc. This does not change the fundamental, qualitative result of the preceding analysis: a binding liquidity constraint makes storage – whether in cash or in kind – less likely. The value of stored grain is proportional to the marginal value of cash over time. As consumption of c_H falls when the liquidity constraint binds, the current marginal utility of c_H increases, making storage so as to increase expected future cash returns less likely.
The credit constraint induced reduction in grain storage also has implications for the household latent supply function over time. When the liquidity constraint binds, demand for storage decreases and the household stocks out of its carryover grain supply. Given these two factors, this implies that the latent carryover supply of grain in the household is extinguished in the periods following a binding liquidity constraint and prior to the next harvest. Because of the fact that realisations of income are stochastic, in seasons where harvest is adequate and the household has no extraordinary expenses, then grain storage is positive (conditional upon preferences and storage costs) and the household can maintain grain supply between seasons so as to take advantage of inter-temporal arbitrage opportunities. But as soon as realised income falls below the income threshold, it is no longer optimal to hold grain stocks as a buffer against future income draws and the household consumes whatever existing grain stores it has on hand.
There is thus also a ‘kinked supply’ curve between harvest realisations that is the analogue to the liquidity-constrained demand curve shown in equation (7). Starting the latent supply curve (labelled q_t next) iterations in the harvest season (initial time t = H), the impact of a binding liquidity constraint at harvest time on household intra-harvest supply is shown in equation (8):

(8)

The effect of the credit constraint on supply is thus, likewise, to decouple current and future production decisions and eliminate the use of storage to maximise expected inter-temporal income and thus utility.

Transaction costs, market participation choice and seasonality 2.1.

Non-trivial transaction costs to market participation are as widespread as liquidity constraints in rural areas of developing countries and similarly create discontinuities in observable behaviours. As de Janvry et al. (1991) explain, transaction costs, τ_t, create a price band around the prevailing market price, p_t. For sellers, the net return per unit output sold (p_st) is the market price (p_mt) minus transactions costs (e.g. p_st≡ p_t − τ_t), while for buyers, the net cost per unit purchased is just the market price plus transactions costs, or p_bt≡ p_t + τ_t.⁷
The household makes its market participation decision whether to be a net buyer of grain (c_t > q_t), a net seller of grain (c_t < q_t) or autarkic in grain (c_t = q_t)⁸ in each period based on a comparison of the indirect utility it would enjoy under each option (Key et al., 2000). The indirect utilities are evaluated at the price appropriate to each market participation regime, p_bt for buyers, p_st for sellers and the non-tradable shadow price, p_t^*, for autarky, determined at the point where internal household demand equals supply, such that p_st ≤ p_t^* ≤ p_bt.
Because of both standard inter-temporal utility maximisation conditions and price risk aversion, in the absence of liquidity constraints, total household grain demand (c_t) should vary inversely with seasonal changes in market prices, falling as one moves from the low-price harvest season to the high-price lean season. Thus, abstracting for the moment from seasonal variation in incomes, for shadow prices, p_H^* > p_L^* while for market prices, p_H < p_L. Assuming constant transactions costs, if it participates in the market at all, the unconstrained household should engage in canonical inter-temporal arbitrage, buying during the low-price harvest season, selling during the higher-price preharvest season or both.
Now consider what happens if the household faces a binding liquidity constraint. The liquidity constrained demand function [c(p_H, w, Y_H(α))], from equation (7), obviously varies directly with the borrowing limit α that determines the threshold income level at which the constraint binds, Y^*(α). This happens because any increase in α enables the household to reallocate consumption to the present and thereby reduce the gap in expected marginal utility of consumption across periods. As household demand for c_t falls, p_t^* necessarily falls as well. Thus, liquidity constraints reduce the household’s shadow price for storable grains. If this effect is sufficiently pronounced, it can induce ‘sell low’ behaviour in the immediate postharvest period.
Figures 1 and 2 illustrate the effect of liquidity constraints on household market participation decisions in the harvest and lean periods, respectively. The figures show latent household demand and supply in shadow price space for a stylised household facing a particular market price, p_t in the both the harvest (H) (Figure 1) and lean (L; Figure 2) seasons. In Figure 1, it can be seen that the liquidity constraint unambiguously lowers the household’s latent demand in the harvest season, and thus p_H^*, thereby increasing the likelihood that the household becomes a grain seller by the fact that p_H^* falls into the indicated ‘sales region’ (where the shadow price is less than or just equal to the market price net of transactions costs, p_H−τ). For the comparable unconstrained farmer, p_H^* falls within the non-tradable band around the given market price (autarkic region) and thus the unconstrained household optimally chooses autarky.⁹ But for the liquidity-constrained households whose shadow price has fallen, it becomes optimal to sell grain, with no change in market price, transaction costs or the household supply schedule. Low price sales at harvest are a product of the household’s binding liquidity constraint.
Figure 1. The impact of liquidity constraints on latent demand and market participation choice in the harvest season (‘sell low’) 

Figure 2. The impact of liquidity constraints on latent supply and market participation choice in the lean season (‘buy high’) 

Figure 2 demonstrates the effect of the binding harvest period liquidity constraint on latent lean season supply, shadow prices and market participation. In the most extreme case shown, the effect of the constraint is to induce a stock-out, thereby reducing latent supply (i.e. carryover stocks) to zero and raising lean season shadow prices, p_L^*. If this effect is large enough, then a credit constraint should lead to increased observations of purchases during the lean season when household stocks are low or gone, in spite of the fact that lean season market prices are higher than the harvest period prices at which the household sold grain owing to the binding liquidity constraint. Hence the ‘sell low, buy high’ phenomenon.
To summarise, given the seasonal nature of storable commodity prices, which typically fall at harvest and rise steadily and predictably over the lean season, ‘sell low’ behaviour clearly turns on either the simple primitives of high discount rates or storage losses, as discussed previously, or liquidity constraints that bind during the harvest period. This is surely not a ubiquitous condition but may occur with some frequency because of some combination of a poor harvest, highly inelastic demand for non-grain items such as school fees, or medical or ceremonial (e.g. funeral, wedding or religious festival) expenses, each of which effectively reduces discretionary income to the point that it falls below Y^*(α). Higher-income households would thus be less likely to sell at postharvest lows and those with extraordinarily high non-discretionary expenses would be most likely.
The ‘buy high’ phenomenon, in contrast, depends on reduced latent grain supplies coupled with high lean season prices. This is especially likely if households stop holding grain stores and stock out because of a binding credit constraint. In the case of individual households, the liquidation of household stores to satisfy consumption requirements can lead to extreme spikes in the household shadow price for grain. If this occurs in the lean season, which seems likely owing to primary income realisation in the harvest period, then it can push credit-constrained, grain-producing households to become grain purchasers, despite high expected prices. Thus the effect of the credit constraint is transferred to market participation behaviour throughout the time between harvest realisations and can lead to rational sales at low prices and subsequent purchases of the same commodity at higher prices. This stylised model brings into stark relief the quite distinct grain marketing choices expected of liquidity-constrained and liquidity-unconstrained households. While existing work on market participation has highlighted the importance of transaction costs and the complicated interconnections between market and non-market activities (de Janvry et al., 1991; Key et al., 2000), this work we believe is the first to introduce an explicit method of examining the seasonal dimensions of market participation for smallholder farm households who may opt out of markets because of positive transaction costs over the course of the year.

Estimation Strategy 3.

The preceding model yields clear, testable hypotheses. By reducing latent household demand in the harvest period, liquidity constraints should decrease the likelihood of (low price) harvest season purchases and increase the likelihood of (low price) harvest season sales, all else equal. Further, households that experience harvest period liquidity constraints should also be more likely to undertake (relatively expensive) lean season purchases and less likely to undertake (high price) lean season sales. We can thus explore empirically the liquidity constraint explanation of the ‘sell low, buy high’ puzzle by testing those hypotheses.
The econometric challenges are that transactions costs create unobserved market participation thresholds, shadow prices are unobservable, market participation behaviours are surely correlated within (i.e. between autarky, buyer and seller status) and across seasons for a given household and transaction volume decisions are not independent of households’ self-selection into the market. One needs to employ an estimation strategy that will address all these thorny econometric issues.
For a single agricultural season, or a single type of market participation (sales or purchases), at least some of these problems can be addressed through the use of standard sample selection models that identify which households participate in markets and correct for the endogeneity of the market participation decision in the estimation of the correlates of observed marketed quantities for participants. These models can be estimated separately for sellers and buyers, or jointly (as was done in Goetz, 1992). Yen’s (2005) multivariate sample selection model (MSSM) is similar to the work of Goetz and others (starting with Lee et al., 1980) but allows for joint estimation of separate parameters across more than two sample selection equations with potentially correlated error structures. In our case, we apply the MSSM to the market entry and quantity decisions for maize grain sales and purchases in both a harvest and a lean season to not only capture the relationship between sales and purchase decisions, but also any potential correlation across harvest and lean seasons. This results in a system of four market entry decision equations (k_sn,i) and four censored market quantity equations (q_sn,i) per household i that correct for sample selection bias in each season and can be summarised as follows:

(9)

where k_sn,i = {0, 1}, s = {harvest (H), lean (L)} and n = {purchase (P), sale (S)}.
The entry decision is assumed to depend upon the (time-invariant) covariates that influence the shadow price through latent demand or latent supply as well as factors influencing the household-specific fixed transaction costs that impact the size of the price band around the market price (Key et al., 2000). The marketed quantity decisions (conditional upon entry) are functions of the factors that influence household latent demand and supply, but are also functions of the (time-varying) market price net of any proportional transaction costs for the particular type of market participation it chooses as optimal.¹⁰ The full specification for the joint entry and quantity equations is therefore¹¹:

(10)

Both market entry and marketed quantities are random variables. Market entry is observed if the entry equation [shown as z_i′α + u_sn,i in equation (10)] is greater than zero. If market entry is observed, then the quantity transacted in the market is given by x′_sn,iβ_sn+ v_sn,i. Both u_sn,i and v_sn,i are assumed to be mean zero, normally distributed random variables. If we let e represent the concatenated vector of the entry and level equation error terms, then the full variance–covariance matrix for the specification is an 8 × 8 matrix, composed of the variance–covariance matrices of the error terms in the market entry and level equations, both within as well as between these equations:

(11)

The full likelihood function is defined by Yen (2005).
The MSSM estimator was initially developed to identify significant covariates of household decisions to purchase a set of consumer goods as well as the quantity purchased in censored demand systems. One identifies the market entry equation by incorporating covariates thought to affect the discrete market participation decision but not the conditional quantity choice. We use the MSSM estimator in a similar way to investigate the significance of household cash liquidity constraints on sales and purchases entry and quantity decisions in the harvest and lean seasons, per the theoretical set-up of section 2. In our case, the identifying variables implied by theory are the fixed transaction costs associated with market entry, which should be irrelevant to the marketed quantity decision conditional on participation (Key et al., 2000).
We face a second identification challenge because our core hypotheses revolve around how liquidity constraints affect market entry and quantity transaction decisions. We operationalise (the absence of) liquidity constraints using the ability to borrow (i.e. access to credit) and access to steady, significant cash flow associated with off-farm income from salaried or skilled employment (or self-employment). Off-farm income is included in our tests for the effect of liquidity as, in the absence of more formal borrowing, households with consistent cash flow from a salary may nonetheless also be able to avoid the ‘sell low, buy high’ marketing pattern as this income is likely to be readily available for non-market purchases (e.g. through holding cash savings). In terms of our model, households with a better ability to cover all consumption expenses adequately, either through readily available cash or borrowing, have incomes consistently above the threshold and therefore avoid such mistimed marketing of their agricultural output.
Finally, because access to credit is likely to be endogenous, we need to instrument for it before testing our core hypotheses. We identify the instrumenting regression for credit access using covariates likely to reflect lenders’ costs of extending credit to a given household and other transaction cost measures likely to be associated with credit access but not with maize market participation. We now explain the data and these variables.

Data 4.

The data, collected by the Tegemeo Institute of Agricultural Policy and Development, come from a 2005 survey of 1,682 households in four districts across 137 villages in western Kenya and report on many aspects of household production, consumption and marketing behaviour, including monthly purchases and sales (and associated prices) over the course of the previous year (i.e. from July 2004 to June 2005).¹² The survey data also contain information on local commodity markets as well as market-based interventions like cereal banks, market information initiatives and a programme designed to increase agricultural credit by extending credit to agricultural input retailers. So as to increase the observation of rare events (e.g. cereal bank membership), the survey design was choice-based rather than a strictly random sample. Therefore, all statistical analysis has been appropriately reweighted to account for the sampling design using techniques found in Manski and Lerman (1977). Summary statistics for the liquidity and market participation variables appear in Table 1. Other key household statistics can be found in Table A1 in the appendix.

Table 1.   Summary statistics
Variable name	Mean	Linearised SE*
Predicted probability of non-agricultural credit usage	0.285	(0.004)
Total off-farm income (×100,000 KSh)†	0.032	(0.002)
Value of grain storage unit (×1,000 KSh)	0.859	(0.319)
Distance to nearest shopping centre (km)	1.727	(0.035)
Prices‡
Harvest season maize grain purchases (KSh/kg)	16.331	(0.093)
Harvest season maize grain sales (KSh/kg)	13.462	(0.115)
Lean season maize grain purchases (KSh/kg)	17.393	(0.046)
Lean season maize grain sales (KSh/kg)	15.702	(0.179)
Marketed quantities
Harvest season maize grain purchases (kg)	58.130	(2.202)
Harvest season maize grain sales (kg)	319.227	(22.261)
Lean season maize grain purchases (kg)	55.892	(1.415)
Lean season maize grain sales (kg)	598.869	(62.839)

Notes: *Linearised standard errors (SE) reported to account for sample design on calculation of sample means.

†Off-farm income is measured over the entire year for all members of the household who had any kind of off-farm salaried employment.

‡Prices and quantities are averaged only over market participants.

Most farmers in the sample engage in rainfed agriculture, on farms of three acres or less. Households grow maize, the staple crop, and either sell or store it on the farm until it is either consumed or sold in the period between harvests.¹³ Typical storage facilities for maize are open bins constructed of wood or bamboo that are raised off the ground to protect the output from pests, or the maize is simply stored in bags inside the family home. In rare cases, a household will have a concrete storage area for grains. Households that belong to cereal banks store some of their output as a share contribution held at the cereal bank, which typically occupies a concrete structure in the local market place. However, the combination of these storage technologies appear to be sufficient to protect households from high storage losses, as over 87% of the maize growing households in the sample report zero losses of harvested maize because of spoilage and the average rate for those experiencing any losses was less than 8%.

Seasonal market participation 4.1.

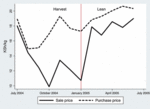
The data collected summarise monthly marketing patterns for the households. However, to make the estimation more tractable and to limit the number of zero observations, we aggregated household market participation into a single, average harvest period and a lean period. Kenya’s western region has bimodal rainfall, with a ‘long rains’ season that runs from April to June (with long rain harvests beginning in July) and a ‘short rains’ season from October to November (with harvests from November to January). For this analysis, we divided the data into a broadly defined ‘harvest period’ (running from July to January) and a ‘lean period’ from February to June, although it technically encompasses two distinct growing seasons. We did this because survey data indicate that over 80% of the households had no stored maize grain at the time of the survey (which occurred at the end of the short rains season) and that most had run out during the month of February. Thus, the stock-out behaviour we wish to study did not occur with great frequency in the period between the long and short rains season.¹⁴ We then calculated an average sale and purchase quantity for each period for households that participated and used these averages in the market participation estimation. We also divided the off-farm income into seasonal averages, so that the estimation represents household average behaviour for harvest and lean period transactions.
Lean season prices were higher than harvest period prices and the purchase price – sales price margin was greater in the harvest season as well (Table 1 and Figure 3); these seasonal differences are statistically significant. Also, according to monthly maize price data available from the Eastern Africa Grain Council’s Regional Agricultural Trade Intelligence Network (RATIN, 2009) between 1997 and 2007 for Kisumu, a nearby large market, the average seasonal price spread for maize over these 11 years was approximately 21%, with positive spreads of between 6% and 75% in 9 of the 11 years.¹⁵

Figure 3. Average maize sale and purchase prices for monthly market participants

For our sample, given mean purchase-sales price differences, there was little money to be made by farmers who bought maize at harvest, stored it for a few months, and resold it in the lean season. But those who sold in the harvest season and bought maize back in the lean season faced an average loss of 29.3% (KSh17.393/KSh13.462) on the inter-seasonal terms of trade, far greater than prevailing local interest rates for those with access to credit. Hence the ‘sell low, buy high’ puzzle.
Yet many indeed follow that practice. Table 2 summarises households’ net maize marketing position per season. Most households were either net buyers of maize in both the harvest and lean seasons, or net buyers only in the lean season. But these pure net buyers aside, the most common pattern was ‘sell low, buy high’, precisely the puzzling pattern we seek to explain. Nearly one in five households was a net seller in the low-price harvest season and a net buyer in the high-price lean season. Ten per cent of the sample was autarkic in both periods, neither buying nor selling maize. Other combinations of seasonal purchase and sales behaviours were practiced by less than 10% of the sample. Only 2% of observations exhibit canonical inter-temporal grain price arbitrage, involving purchases in the low-price harvest period and sales in the high-price lean season. Of the nearly 30% of the sample that were net sellers in the harvest period, an astonishing 62% were net buyers a few months later, raising the obvious question of why they would choose a nearly 30% loss on the maize they sold immediately postharvest and then bought back in the lean season. Furthermore, these marketing patterns were observed for nearly every village within the sample, as there were households that chose to ‘sell low, buy high’ in 113 of 137 villages and inter-seasonal price variation was on a similar order of magnitude across the sample.¹⁶

Table 2.   Frequency of maize marketing regimes
Marketing regime (harvest-lean)	Frequency	Percentage of sample
Net buyer–net buyer	550	33
Net seller–net buyer	300	18
Autarkic–net buyer	327	19
Net buyer–net seller	38	2
Net seller–net seller	73	4
Autarkic–net seller	79	5
Net buyer–autarkic	36	2
Net seller–autarkic	114	7
Autarkic–autarkic	165	10
Total	N = 1,682	100%

Household credit access 4.2.

Households were asked whether or not they received credit (in cash or in kind) for agricultural inputs as well as any credit obtained for non-agricultural purposes. For agricultural credit, the data is binary, simply yes or no, while for non-agricultural credit, households were asked whether or not they applied for a loan to cover any non-agricultural expense (like school fees or another similar item), whether or not they were successful in their application and how much they received. Because of the fungibility of credit and the binary nature of the agricultural credit data, we created a single dummy variable indicating reported credit use, whether for agricultural or non-agricultural purposes. We use credit use as a proxy for credit access.
It is important to note that we cannot precisely distinguish the credit constrained from the non-constrained given the data available. More informal sources of credit, such as extended family or local community groups, are not covered by the data and we do not know if people who received credit were nonetheless quantity rationed in the volume received or if those who did not receive credit had no need for it. Our credit use variable is thus an imperfect proxy for the true variable of interest (the absence of) liquidity constraints by virtue of credit access but is the best available, given the data.
To account for the possible endogeneity of the credit use dummy variable, we predict credit use probabilities for each household in the sample using a probit model instrumenting regression, and then use these predicted values in the second-stage MSSM model of market participation decisions. We follow Kochar (1997) and characterise this first-stage equation as representing the difference between a household’s marginal return from using credit and the marginal cost to a lender of providing it. We therefore include several household demographic variables and distance measures¹⁷ to control for household credit demand as well as variables that are associated with potential household collateral (income and land owned) and monitoring (experience) that might reduce the costs of credit for lenders as identifying variables.
The results of the first-stage probit estimation on credit usage are included in the appendix (Table A2). As one would expect, credit use is strongly and statistically significantly increasing in household income, in household labour endowments, longevity in the village, in the educational attainment of the household head. The identifying vector of distance variables is jointly statistically significant and generally exhibits the expected, negative point estimates, indicating that proximity to places where one commonly finds (typically micro) financial institutions in rural western Kenya fosters greater credit access. The one curious exception is distance to a health centre, which is positively and significantly correlated with credit use, which likely reflects the low density of health centres in the region.

Econometric Results 5.

As indicated previously, the core hypotheses of interest concern the coefficient estimates on our two variables reflecting household liquidity: predicted probability of credit use and household off-farm income.¹⁸ With respect to the four market entry equations, we expect that household liquidity should reduce the probability of harvest period sales and lean season purchases, and increase the probability of harvest season purchases and lean season sales. The literature on market participation indicates parallel predictions with respect to the volume equations, although without detailed income data to fully control for income effects, we are less confident about those point estimates than about the market entry decision estimates. Tables 3–4 display the estimates from the entry and quantity equations, respectively, while Table 5 contains the various cross-equation covariance estimates between the entry and quantity equations.¹⁹

Table 3.   Multivariate sample selection model estimates of market entry by season
	Entry decision equationsa
	(HP)	(HS)	(LP)	(LS)
Liquidity measures
Predicted probability of credit use	2.918 (1.200)**	−3.277 (1.194)***	−0.7142 (1.209)	−3.351 (2.075)
Off-farm income (1 × E6 KSh)	−8.899 (2.832)***	−2.839 (2.751)	−7.579 (2.654)***	5.308 (3.395)
Supply shifters
Total acres owned	−11.766 (2.323)***	8.301 (1.882)***	−7.413 (1.864)***	7.279 (2.567)***
Weather shock (1 = planted late)	−0.439 (0.355)	0.410 (0.352)	−0.329 (0.332)	0.948 (0.603)
Storage container value (×1,000 KSh)	−2.614 (31.061)	−8.088 (22.509)	−15.753 (26.262)	27.431 (38.962)
Demand shifters
Age of household head (years)	−0.141 (0.765)	−1.480 (0.735)**	−0.691 (0.684)	−1.089 (1.247)
Gender of household head (1 = male)	−0.082 (0.371)	−0.054 (0.386)	−0.772 (0.364)**	0.851 (0.730)
Dependency ratio	1.581 (1.224)	0.717 (1.255)	−0.120 (1.273)	0.547 (2.218)
Some formal education (1 = yes)	0.268 (0.424)	0.484 (0.458)	0.489 (0.389)	0.199 (0.958)
More than high school (1 = yes)	0.154 (0.755)	1.199 (0.760)	0.099 (0.708)	−0.035 (1.382)
Transaction costs
Distance to market shops (km)	2.497 (0.986)**	0.379 (1.017)	0.948 (0.982)	−0.297 (1.465)

Notes: ^aN = 1682. Standard errors are in parentheses. District dummy variables and the constant are included but not reported. Data have been scaled to remain within the range {0, 1} as follows: x_scaled = (x−x_min)/(x_max−x_min) (Lapedes and Farber, 1988). *, ** and *** indicate significances at 10%, 5% and 1% levels, respectively. The entry equation variances have been normalised to 8 to allow for numerical evaluation of the likelihood function. Mean log-likelihood = −10,122. Likelihood ratio statistic (χ²(56)) = 1,947,756; P = 0.000.

Table 4.   Multivariate sample selection model estimates of market quantity by season
				Quantity decision equationsa
				(HP)		(HS)			(LP)		(LS)
Liquidity measures
Predicted probability of credit use				1.255 (0.196)***		0.143 (0.606)			1.035 (0.160)***		−0.116 (0.755)
Off-farm income (1 × E6 KSh)				1.326 (0.568)**		1.192 (1.286)			1.258 (0.382)***		1.731 (1.536)
Supply shifters
Total acres owned				−0.047 (0.470)		2.864 (1.195)**			0.327 (0.277)		2.793 (1.230)**
Weather shock (1 = planted late)				0.100 (0.065)		0.041 (0.146)			0.126 (0.051)**		0.321 (0.292)
Storage container value (×1,000 KSh)				−1.185 (6.752)		0.601 (8.722)			4.075 (5.148)		−3.365 (3.158)
Demand shifters
Age of household head (years)				0.203 (0.134)		0.518 (0.338)			0.242 (0.103)**		0.028 (0.491)
Gender of household head (1 = male)				0.304 (0.061)***		0.339 (0.154)**			0.239 (0.052)***		0.056 (0.339)
Dependency ratio				0.299 (0.231)		−0.454 (0.480)			0.171 (0.171)		−1.251 (0.851)
Some formal education (1 = yes)				0.030 (0.073)		0.615 (0.209)***			0.120 (0.055)**		0.991 (0.337)***
More than high school (1 = yes)				−0.331 (0.131)**		1.024 (0.336)***			−0.190 (0.106)*		1.432 (0.502)***
Market prices
Prices (KSh/kg)				−1.163 (0.173)***		1.773 (0.445)***			−1.084 (0.200)***		0.162 (0.697)
Note: aSame as in Table 3. Table 5.   Estimated error covariances: entry-to-entry [ E(usn,usn)], entry-to-level [E(usn,vsn)] and level-to-level [E(vsn,vsn)] (sn = HP, HS, LP, LS)
	uHP	uHS	uLP		uLS		vHP	vHS		vLP		vLS
uHP	–	−0.999 (0.928)	0.892 (0.896)		−0.999 (1.532)
uHS	–	–	−0.888 (1.104)		0.994 (1.779)
uLP	–	–	–		−0.999 (1.080)
uLS	–	–	–		–
vHP	0.703 (0.366)*	−0.586 (0.105)***	−0.703 (0.103)***		−0.703 (0.238)***		0.495 (0.030)***	0.015 (0.088)		0.286 (0.027)***		0.094 (0.129)
vHS	−0.900 (0.186)***	1.081 (2.916)	−0.623 (0.171)***		−0.113 (0.372)		–	1.168 (0.285)***		0.095 (0.059)		0.592 (0.113)***
vLP	−0.648 (0.092)***	−0.374 (0.090)***	0.648 (0.269)**		−0.648 (0.138)***		–	–		0.421 (0.018)***		0.052 0.092
vLS	−1.051 (0.356)***	−0.110 (0.362)	−1.051 (0.243)***		1.051 (1.806)		–	–		–		1.105 (0.216)***

Notes: *, ** and *** indicate significances at 10%, 5% and 1% levels, respectively.
The coefficient estimates on our two measures of liquidity, predicted credit access and off-farm income, are jointly consistent with our hypothesis that households with sufficient access to liquidity successfully avoid selling low and buying high in the maize market. Credit use is associated with reducing the likelihood of market entry as sellers in the harvest period and off-farm income are associated with reduced likelihood of purchases in the lean period. Further, predicted credit use is significantly associated with an increased likelihood of harvest season purchases. The lack of significance for either liquidity measure on lean period sales is possibly due to the fact that sample households are overwhelmingly net maize buyers and thus sales of any sort are not expected. The different forms of household liquidity have similar estimated effects on marketed quantities. Households using credit and with larger off-farm incomes transact more in the market than those without. This may well pick up omitted income effects. Overall, while the results are not entirely clear-cut, the evidence clearly supports the hypothesis that liquidity constraints drive households to practice the ‘sell low, buy high’ maize marketing strategy in rural Kenya.
Our confidence in the parameter estimates of interest concerning the effects of liquidity on grain marketing is buttressed by the fact that the other parameter point estimates are also consistent with expectations. For example, the entry coefficients for total acres owned show that households with more land holdings are more likely to sell and less likely to buy maize in either season, and once part of the market, these same households tend to transact in larger quantities than those with smaller land sizes with the exception of harvest period purchases. This makes intuitive sense if these households are simply producing more on their land and therefore enjoy larger marketable surpluses. This surplus allows larger sales quantities in both periods, as well as greater ability to consume out of own production at harvest time. For lean period purchases, these households may also benefit from greater income earned during the year, which may boost lean period purchases.
Prices significantly influence marketed quantities in the manner expected except for lean period sales, but again, this is likely to be because of the fact that lean period sales are not frequently observed. Additionally, the implied own-price demand elasticities are 0.77 and 0.83 for the harvest and lean seasons, respectively, and for supply, they are 1.09 and 0.12 (harvest and lean). Both sets of elasticity estimates are in line with others reported elsewhere for the region.²⁰ The signs of the estimates on greater storage capacity suggest that households with better storage facilities tend to participate less in the market overall, although this relationship is not statistically significant. This fact aligns with previous work on the role of grain storage already cited before (Barrett and Dorosh, 1996; Park, 2006).
Other correlates seem to more precisely impact market quantity decisions, rather than entry decisions. For example, although gender does not seem to greatly influence market entry, male-headed households tend to transact in larger quantities in the market for both sales and purchases than female-headed households. This may reflect some general differences in wealth or market information networks between these two groups. Also, households where the head has had some formal education tend to transact in larger quantities, although the highest educated households sell more and purchase less than the average, possibly indicating that these households are more commercially oriented or are achieving some additional benefits to education in terms of higher on-farm yields.
The cross-equation covariances provide additional evidence on the relationships between harvest and lean period market participation decisions. Although the covariances between entry equations are not well identified, the diagonal elements in the matrix of covariances from entry-to-level equations are analogous to the inverted Mills ratios that are often calculated as part of typical univariate Heckman models of sample selection. We can therefore see from these estimates that households in the market in general transact more than a randomly selected household, as all of the entry-to-level covariances on the diagonal are positive. We can also see this by looking at the level-to-level covariances, which are all positive, indicating that both sales and purchase quantities are positively correlated for market participants. Overall, the statistical significance of many of the cross-equation covariance estimates underscores the importance of estimating these behavioural equations using a systems approach such as MSSM.
A few of the parameter estimates run counter to intuition. The mostly positive point estimates on transaction costs seem to indicate that households farther from markets are more likely to make transactions in markets. However, Renkow et al. (2004) found little relationship between distance to market and transaction costs for villages in Kenya without access to motorised transport. It is possible, therefore, that our parameter estimates are capturing some other features of our sample villages such as those that lie behind the results in Renkow et al., and our distance variable is thus only an imperfect proxy for fixed transaction costs. However, we are not able to include specific transport types in our estimates, and are limited in our ability to explore this issue further without additional primary research.
A final point on the presented estimates concerns the validity of the standard errors. As we have used predicted credit as a regressor in the final estimation of the MSSM, an appropriate solution is typically the use of bootstrapping techniques (Horowitz, 2001) to produce consistent standard errors. However, given the fact that the dependent variable in the first stage is binary, bootstrapping in our case produced a high number of samples that could not be used to estimate the model, as there were no observations of individuals with access to credit in the replication sample produced by the bootstrap procedure. Therefore, the standard errors have not been corrected to account for the presence of the generated regressor, because of the infeasibility of the usual corrective with our particular model, and the absence of other acceptable alternatives. The fact that our univariate results on the main parameters of interest are qualitatively similar to those presented here suggests that this should not greatly alter the inferences made from the multivariate model.

Conclusions 6.

This article explores empirically the oft-observed ‘sell low, buy high’ puzzle of smallholder food marketing behaviour, based on the hypothesis that liquidity constraints drive poor households to use commodity markets as a substitute for financial markets to which they have limited or no access. Although considerable, predictable seasonal increases in grain prices should dissuade households from selling staples at low prices postharvest and buying them back again a few months later, we find that 18% of a recent sample of smallholder households in rural western Kenya in fact practice the ‘sell low, buy high’ strategy. As noted by Park (2006, p. 1088), grain stores maintained from harvest to harvest are typically used as a price hedge to ensure adequate consumption. In contrast, a ‘sell low, buy high’ behaviour between harvests would seem to reflect not only an inability to hedge, but liquidity constraints that compel households to quasi-borrow by liquidating physical grain inventories in an inter-seasonally unprofitable fashion.
Using an adaptation of a recently developed censored demand systems estimator, we reject the hypothesis that liquidity has no effect on household marketing patterns in favour of the alternate hypothesis that it indeed reduces the likelihood of selling low or buying high. While the quantity parameter estimates vary depending on the kind of liquidity to which the household may have access, the market entry parameter estimates (that are more reliable in these data) are broadly consistent with the model we lay out. Other parameter estimates largely make sense as well.
The practical concern, of course, is that households who engage in ‘sell low, buy high’ behaviour use up scarce resources in costly grain market transactions, making it more difficult for them to accumulate resources necessary to invest in productive assets or improved technologies so as to sustainably increase incomes. Thus not only do these seasonal flow reversals reflect lower welfare just as they do at more aggregate levels (Barrett and Dorosh, 1996, p. 636) they also reflect displaced financial market failures that can trap households in long-term poverty through distorted grain marketing patterns.

Footnotes

·         2

See Barrett (2007). However, this is not a universally widespread phenomenon, as Alderman and Shively (1996) show for Ghana.

·         3

These losses could be due either to biophysical deterioration or loss of commodities or to claims made on stored grains by family and friends, that is, implicit social taxation of storage.

·         4

It should be noted that the rates in Barrett (1997) are for rice, which tends to be less susceptible to pests than maize. However, the storage loss rates observed in the maize data used in this article are still far below observed maize price spreads.

·         5

Because of the very low level of fertiliser usage in the region (Duflo et al., 2008), we are ignoring non-labour inputs for simplicity.

·         6

These functions are also conditional on the household’s tastes, discount rate and local prevailing interest rates. This stylised version of household inter-seasonal behaviour does not incorporate the impact of changing food consumption on income, as in Behrman et al. (1997b).

·         7

We temporarily ignore fixed transaction costs for ease of exposition.

·         8

We assume that the storage decision is implicit in the market participation decision. This is justified by the fact that household latent supply, which contributes to the household shadow price determination, is a function of the household’s storage decision.

·         9

It is also possible that for unconstrained households, latent demand is sufficiently high that grain purchases are the optimal marketing regime.

·         10

The households in our sample are conducting market transactions at very small quantities. Therefore, in practice, we are only considering fixed transaction costs in the entry decision in our estimation.

·         11

The logarithmic transform of the marketed quantity variable, q_t, is used to avoid having to compute the multivariate likelihood function using a truncated normal distribution for strictly positive marketed quantities. This is a common simplification used in other studies of multivariate censored demand systems (Jones, 2000; Yen, 2005).

·         12

Further information about the institute can be found on their website: http://www.tegemeo.org.

·         13

Households also grow some cash crops. Because of possible endogeneity in the crop portfolio decision and a lack of suitable instruments, we are unable to directly control for these other crops in our specification. However, Park (2006) has demonstrated that households growing both grain and cash crops should still primarily use their grain stocks as a hedge against consumption risk. Further, we do include information on off-farm income from salaried employment in our model and use it as a proxy for all other sources of household cash liquidity, including income generated by cash crops. We ran a separate estimation with cash crop income included as part of the off-farm income variable. This did not significantly impact the estimated parameters, which suggests our more limited off-farm income variable is likely to be the best proxy for liquidity from all forms of cash income, including from cash crops.

·         14

Defining seasons in this manner also increased the total number of observations of each of the four types of market participation.

·         15

In the two years with negative spreads, prices fell between 4% and 14%.

·         16

Unfortunately, we do not have data on specific maize varieties or other quality measures to provide additional insight into the inter-seasonal price spreads. However, given that many of the farmers sampled belong to cereal banks that pool harvested maize and sell it from central markets to either commercial millers or to individuals in small quantities for home consumption, it is likely that the same varieties of maize that these farmers grow on their farms is being sold for consumption in the local market in most cases. In this case, the seasonal fluctuations in local maize supply and demand are likely the main cause of the inter-seasonal price variation, rather than quality differences.

·         17

Distances from financial institutions have been shown in previous work to affect borrowing behaviour (Behrman et al., 1997a) and thus we are using distances to markets, piped water, etc. as proxies for possible distances to other kinds of infrastructure and institutions, like banks.

·         18

Off-farm income could be endogenous to market participation and volume decisions as well. But as we use exclusively salaried and skilled, year-round employment, this is likely predetermined when households made their 2005 marketing decisions. Moreover, the data have no suitable instruments to identify this variable separately from the market entry and credit use variables, so we have no viable options for resolving any prospective endogeneity in the off-farm income variable.

·         19

We obtained qualitatively similar results with a univariate specification for each of the market participation equations, which are available upon request. They have been omitted here in the interests of brevity. We estimated the multivariate model using GAUSS 9.0. The necessary multivariate cumulative distribution functions were evaluated with the Geweke-Hajivassiliou-Keane (GHK) simulator (Hajivassiliou, 1997).

·         20

Given the linear scaling method we use to facilitate the model estimation (Lapedes and Farber, 1988), the conditional price elasticity for each season is calculated as: e^c = price_meanβ/(price_max − price_min), where β is the estimated model parameter.

References

·         Alderman, H. and Shively, G. Economic reform and food prices: Evidence from markets in Ghana’, World Development, Vol. 24, (1996) pp. 521–534.

o    CrossRef,

o    Web of Science® Times Cited: 15

·         Antle, J. M. and Capalbo, S. M. Econometric-process models for integrated assessment of agricultural production systems’, American Journal of Agricultural Economics, Vol. 83, (2001) pp. 389–401.

Direct Link:

·         Barrett, C. B. Food marketing liberalization and trader entry: Evidence from Madagascar’, World Development, Vol. 25, (1997) pp. 763–777.

o    CrossRef,

o    Web of Science® Times Cited: 36

·         Barrett, C. B. Displaced distortions: Financial market failures and seemingly inefficient resource allocation in low-income rural communities’, in E.Bulte and R.Ruben (eds.), Development Economics between Markets and Institutions: Incentives for Growth, Food Security and Sustainable Use of the Environment (Wageningen: Wageningen Academic Publishers, 2007, pp. 73–86).

·         Barrett, C. B. and Dorosh, P. Farmer’s welfare and changing food prices: Non-parametric evidence from rice in Madagascar’, American Journal of Agricultural Economics, Vol. 78, (1996) pp. 656–669.

o    CrossRef,

o    Web of Science® Times Cited: 33

·         Behrman, J., Foster, A. and Rosenzweig, M. R. Dynamic savings decisions in agricultural environments with incomplete markets’, Journal of Business and Economic Statistics, Vol. 15, (1997a) pp. 282–292.

o    CrossRef,

o    Web of Science® Times Cited: 3

·         Behrman, J., Foster, A. and Rosenzweig, M. R. The dynamics of agricultural production and the calorie–income relationship: Evidence from Pakistan’, Journal of Econometrics, Vol. 77, (1997b) pp. 187–207.

o    CrossRef,

o    Web of Science® Times Cited: 15

·         Bellemare, M. and Barrett, C. B. An ordered Tobit model of market participation: Evidence from Kenya and Ethiopia’, American Journal of Agricultural Economics, Vol. 88, (2006) pp. 324–337.

Direct Link:

·         Central Bank of Kenya. Annual Report, (Nairobi, 2004).

·         Deaton, A. Saving and liquidity constraints’, Econometrica, Vol. 59, (1991) pp. 1221–1248.

o    CrossRef,

o    Web of Science® Times Cited: 303

·         Duflo, E., Kremer, M. and Robinson, J. How high are rates of return to fertilizer? Evidence from field experiments in Kenya’, American Economic Review, Vol. 98, (2008) pp. 482–488.

o    CrossRef,

o    Web of Science® Times Cited: 8

·         Goetz, S. J. A selectivity model of household food marketing behavior in Sub-Saharan Africa’, American Journal of Agricultural Economics, Vol. 74, (1992) pp. 444–452.

o    CrossRef,

o    Web of Science® Times Cited: 58

·         Hajivassiliou, V. A. A Library of GAUSS Routines for Simulating Multivariate Normal Rectangle Probabilities and their Derivatives. Retrieved 11 August 2010 from http://econ.lse.ac.uk/staff/vassilis/pub/simulation/gauss/simprog.gcf, 1997.

·         Horowitz, J. L. The bootstrap in econometrics’, in J. J.Heckman and E. E.Leamer (eds), Handbook of Econometrics, Vol. 5 (Amsterdam: Elsevier Science, 2001, pp. 3159–3228).

·         IGAD. Intergovernmental Authority on Development, Market Information System Database. Retrieved 11 August 2010 from http://www.adwebtec.it/igadmis/mis/nmis/kenya/timeseries1.html, 2007.

·         de Janvry, A., Fafchamps, M. and Sadoulet, E. Peasant household behavior with missing markets: Some paradoxes explained’, Economic Journal, Vol. 101, (1991) pp. 1400–1417.

o    CrossRef,

o    Web of Science® Times Cited: 201

·         Jones, A. M. Heath econometrics’, in A. J.Culyer and J. P.Newhouse (eds.), Handbook of Health Economics, Vol. 1A, Ch. 6 (Amsterdam: North Holland, 2000, pp. 265–344).

·         Key, N. E., Sadoulet, E. and de Janvry, A. Transactions costs and agricultural household supply response’, American Journal of Agricultural Economics, Vol. 82, (2000) pp. 245–259.

Direct Link:

·         Kochar, A. An empirical investigation of rationing constraints in rural credit markets in India’, Journal of Development Economics, Vol. 53, (1997) pp. 339–371.

o    CrossRef,

o    Web of Science® Times Cited: 32

·         Lapedes, A. and Farber, R. How neural nets work’, in D. Z.Anderson (ed.), Neural Information Processing Systems (New York: American Institute of Physics, 1988, pp. 442–456).

·         Lee, L.-F., Maddala, G. S. and Trost, R. P. Asymptotic covariance matrices of two-stage Probit and two-stage Tobit methods for simultaneous equations models with selectivity’, Econometrica, Vol. 48, (1980) pp. 491–504.

o    CrossRef,

o    Web of Science® Times Cited: 124

·         Manski, C. F. and Lerman, S. R. The estimation of choice probabilities from choice-based samples’, Econometrica, Vol. 45, (1977) pp. 1977–1988.

o    CrossRef,

o    Web of Science® Times Cited: 324

·         Park, A. Risk and household grain management in developing countries’, The Economic Journal, Vol. 116, (2006) pp. 1088–1115.

Direct Link:

o    Abstract

o    Full Article (HTML)

o    PDF(295K)

o    References

·         RATIN. Regional Agricultural Trade Intelligence Network, Monthly Price Data. Retrieved 11 August 2010 from http://www.ratin.net/priceinfo.asp, 2009.

·         Renkow, M., Hallstrom, D. and Karanja, D. Rural infrastructure, transactions costs and market participation in Kenya’, Journal of Development Economics, Vol. 73, (2004) pp. 349–367.

o    CrossRef,

o    Web of Science® Times Cited: 12

·         Saha, A. A two-season agricultural household model of output and price uncertainty’, Journal of Development Economics, Vol. 45, (1994) pp. 245–269.

o    CrossRef,

o    Web of Science® Times Cited: 12

·         Saha, A. and Stroud, J. A household model of on-farm storage under price risk’, American Journal of Agricultural Economics, Vol. 76, (1994) pp. 522–534.

o    CrossRef,

o    Web of Science® Times Cited: 6

·         Sahn, D. E. (ed.), Seasonal variability in Third World agriculture (Baltimore: Johns Hopkins University Press, 1989).

·         Schechtman, J. and Escudero, V. Some results on an “income fluctuation problem” ’, Journal of Economic Theory, Vol. 16, (1977) pp. 151–166.

o    CrossRef,

o    Web of Science® Times Cited: 39

·         Williams, J. C. and Wright, B. D. Storage and Commodity Markets (New York: Cambridge University Press, 1991).

o    CrossRef

·         Yen, S. T. A multivariate sample-selection model: Estimating cigarette and alcohol demands with zero observations’, American Journal of Agricultural Economics, Vol. 87, (2005) pp. 453–466.

Direct Link:

·         Zeldes, S. Consumption and liquidity constraints: An empirical investigation’, The Journal of Political Economy, Vol. 97, (1989) pp. 305–346.

Appendix

Table A1 Summary statistics

Variable name	Mean	Linearised SE
Age of household head (years)	51.380	(0.427)
Gender of household head (1 = male)	0.798	(0.011)
Dependency ratio*	1.011	(0.023)
Head has some formal education† (1 = yes)	0.751	(0.012)
Head has more than high school (1 = yes)	0.082	(0.007)
Total acres owned	2.310	(0.074)
Weather shock‡ (1 = yes)	0.167	(0.010)
Distance to nearest fertiliser seller (km)	3.642	(1.222)
Distance to nearest seller of hybrid maize seed (km)	2.251	(0.049)
Distance to a tarmac road (km)	4.368	(0.119)
Distance to the health centre (km)	2.496	(0.052)
Distance to electricity (km)	3.411	(0.110)
Distance to public telephone (km)	2.432	(0.054)
Distance to obtain extension advice (km)	4.211	(0.091)
Distance to piped water (km)	3.667	(0.11)
District fixed effects	Frequency	% of sample
Number of households in Bungoma District	591	35.1
Number of households in Butere-Mumias District	210	12.5
Number of households in Siaya District	388	23.1
Number of households in Vihiga District	493	29.3

Notes: SE, standard error.

*Dependency ratio is defined as ratio of children less than 15 years old plus adults over 65 years old to all other adults in the household.

†Comparison case is household heads without any formal education.

‡This is a 0-1 variable indicating whether or not a household performed any crop planting tasks late because of bad weather (self-reported).

Table A2 First-stage probit for probability of credit use (=1 if households obtained credit)

Variable name	Estimatea	SE
Total yearly earnings from household members who earn salaried wages (×1,000 KSh)	0.002	(0.001)***
Total acres owned	0.024	(0.016)
Years household has been farming in the village	0.008	(0.004)***
Household size (number of members)	0.036	(0.013)***
Age of household head (years)	−0.007	(0.004)*
Gender of household head (1 = male)	−0.092	(0.109)
Head has no formal education (1 = yes)	−0.242	(0.129)*
Head has some formal education (1 = yes)	0.348	(0.144)**
Distance to a tarmac road (km)	−0.014	(0.012)
Distance to a health centre (km)	0.057	(0.021)***
Distance to electricity (km)	0.008	(0.011)
Distance to public telephone (km)	−0.059	(0.030)*
Distance to obtain extension advice (km)	0.007	(0.014)
Distance to piped water (km)	−0.014	(0.014)
Distance to nearest fertiliser seller (km)	−0.002	(0.000)***
Distance to nearest certified maize seller (km)	−0.038	(0.028)

Notes: SE, standard error.

^aRobust standard errors are in parentheses. *, ** and *** indicate significances at the 10%, 5% and 1% levels, respectively. Division fixed effects are included but not reported; N = 1682; pseudo-R² = 0.1124.

Sumber Referensi :

http://onlinelibrary.wiley.com/doi/10.1111/j.1477-9552.2010.00274.x/full